환영합니다, Rolling Ress의 카루입니다.
문과 학교에서 이과생으로 살아남기.. 그래요. 제 스스로도 미친 짓이라고 생각합니다. 그리고, 그게 힘들다는 것도 알아요. 제가 계속 번복을 하긴 했지만, 뭐... 엄청난 노가다라는 사실은 변하지 않아요. 저도 그걸 알고 있기에, 제 안에서도 혼란이 계속 되는 겁니다.
문과 학교. 문과 수업. 문이과가 통합되었다고는 하지만 국제고의 경우 결국은 "특수목적"고등학교이기에, 그 "특수목적"에 부합하는 교육과정을 따르게 됩니다. 즉, 자연 과목 비중을 줄이고 그 자리에 언어, 지리, 역사, 문화 등 인문계 과목들을 많이 편성하는 거죠. 고양국제고도 그렇습니다.
물론, 그렇다고 문과쪽에만 치중한 과목들이 있는 건 아닙니다. 우리도 과학I 배운다고요 II가 없어서 그렇지 특히 최근에 생긴 GIS (공간정보와 공간분석) 과목이라든지, 내년부터 다시 개설될 미적분이라든지, 정보 과목의 강화형인 창의적문제해결기법이라든지, 탄력적이긴 합니다.
그렇다면 저같은 학생이 할 수 있는 건 무엇이냐? 수행평가에서 이것저것 융합하는 겁니다. 어떻게요? 관심분야를 살려서요. 예를 들자면, 저는 대부분의 수행평가에서 수리 및 과학 분야를 주제로 잡습니다. 독서를 예시로 들어볼게요. 저는 '인공지능과 법' 책을 읽고 탐구 주제를 정한뒤, 텍스트를 바탕으로 다양한 논문을 찾아 분석하며 탐구를 합니다. 그리고 발표 및 토론까지 함께하죠. 비교문화에선 '과학기술과 문화변동'을 주제로 4차 산업혁명이 어떻게 우리 사회를 변화시켰는지 조사하고 발표합니다. 토의도 같이 하고요.
이런 식입니다. 나를 표현할 수 있는 길은 수행평가 뿐. 그리고 이러한 활동은 생기부 세특에 들어갑니다. 내가 잘 하면, 그 모습을 생기부에 담을 수 있어요. 물론 저는 이렇게 보이는 제 모습이 전부라는 게 원통할 뿐. 뭐 어쩌겠습니까. 내가 바꿀 수 없으면, 그냥 닥치고 받아들여야 해요. 전 이걸 깨닫는 데 너무 오래 걸렸습니다.
그렇다면, 진짜 이과 과목들에선 뭘 할까요? 저는 화학I 에서 물에 대한 탐구를 했습니다. "아니, 널리고 널린 것중에 왜 하필 물이냐?" 물은 생각보다 만만치 않거든요. 수소 결합... 화학 II에 나오는 개념들을 엮어서 아주 깊게 탐구한 뒤 보고서로 제출했죠.
그리고 지금 진행중인 수학. 아... 회귀분석으로 삼차함수를 도출해서 수학적으로 분석하는 수행평가가 있거든요? 근데... 망한 것 같아요. 아니, 사실 아무 함수나 상관 없다고 하셨습니다. 미분 가능성, 연속 여부, 접선, 극대/극소 등등...
근데, 거기서 제가 무슨 함수를 골랐는지 아세요? ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ하... 인공지능을 가지고 여러 과목들과 융합하고 있는데, 제가 좀 정신이 나갔는지 활성함수를 골랐습니다. 무슨 함수냐고요? 시그모이드. 특히 로지스틱 함수입니다.

이렇게 생겼습니다. 근데 보시면 아시겠지만, 초월함수입니다. 그니까 원래 고양국제과면 다룰 일이 없었어야 할 함수.. (미적분 과목이 없었을 때는 그랬죠) 근데 뭐 저는 애초에 3학년 때 미적분을 수강하기도 하고.. 그냥 그런지라 했습니다. 참고로 선생님께서는 저보고 "감당할 수 있으면 하라"라고 하셨습니다. 근데 그걸 감당을 할 수 있었을까요.
이걸 이제 수학적으로 분석을 해야 합니다. 증가/감소를 판별하거나, 극대/극소를 추론하거나, 접선을 그린다거나.. 뭐가 많아요. 근데, 다항함수 미분은 간단하죠. 우선 각 항에 대해 미분한 다음 결과를 합하면 됩니다.
f(x) = 3x² + 2x + 1 이걸 미분하면,
f'(x) = 6x + 2가 되죠.
자 그런데... 초월함수의 미분은 그리 간단하지 않습니다. 애초에 지수, 로그, 유리함수들을 미분한다..는 것도 각기 다른 공식들을 기억해야 하기 때문에 좀 까다롭죠. 그리고... 무엇보다 저는 평균변화율의 극한값을 이용해서 미분계수를 도출해내지 못하겠습니다. 선행..이 이럴 때는 꼭 필요하네요. 저런.
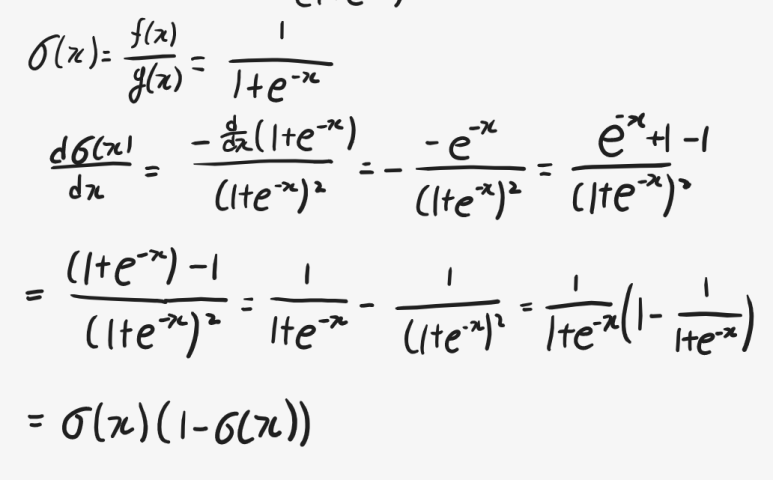
시그모이드 함수를 σ(x)라고 할때, 그 도함수 σ'(x)는 σ'(x) = σ(x){1-σ(x)}가 됩니다. 풀이 과정은 위와 같아요.
수학과제탐구 시간도 재미있습니다. 괴델의 불완전성 정리에 대해 발표한 팀이 있었는데, 괴델수를 가지고 표현하는 것도 상당히 흥미로운 부분이었습니다. 괴델수가 뭐냐? 쉽게 말해 해시값이라고 보면 됩니다. 직접 복호화는 불가능하더라도 뭔지 유추할 수 있는 정도의 해시값. 그 해시값(괴델수)를 통해 Dem(x, y), Sub(a, b, c) 함수를 통해 이런저런 논리를 펼치는데, 이게... 참....ㅋㅋㅋㅋㅋㅋㅋㅋ
발표자 친구에 따르면, 이게 연속체 가설과도 연계가 된다고 합니다. 제가 중학교 때, 그러니까 2020년 1월~2월쯤에 "(0, 1)의 실수의 개수는 실수 전체의 개수와 같다"라는 것에 대해 토론을 좀 해봤거든요. 영재고 친구 한 명, 과학고 친구 한 명, 그리고 뼈이과 친구 한 명, 그 다음 저, 카루입니다. 이렇게 네 명이서 다양한 이야기를 나누었는데, 일단은 y = tan x를 적당히 조정하기만 해도 정의역과 치역을 적당히 조절해서 증명할 수 있습니다. 그런데, 저는 여기서 만족하지 않고 굳이굳이 연속체 가설을 끌어오면서 머리를 터뜨렸죠.

당시 상황입니다만, 자세한 건 나중에 정리해서 올리도록 하죠
"전체는 부분보다 크다"라는 명제가 있다.
만일 존재가 전체와 부분으로 나뉠 수 있다면
이 명제는 증명될 필요가 없으나
공리는 실제와 크기를 끊임 없이 무시한다.
- 칸토어
칸토어 정리, 괴델의 불완정성 정리, 연속체 "가설"... 우리가 일상에서 접하는 수학과는 정말 거리가 멉니다. 근데, 한 가지 치명적인 단점이 있다면 너무 재밌어요. 몰두하게 만듭니다.
연속체 가설에 관한 내용은 나중에 NOCHES 글로 따로 정리하겠습니다. 아무튼, 참 이런 수행만 하다보면 좋은데, 지필평가가 제 발목을 잡네요. 기계적으로 문제를 푸는 것이 과연 올바른 길일까.. 개념을 정확히 파악하고 다른 곳과 융합할 수 있는 창의력이 훨씬 중요한 게 아닌가.. 근데 적어도 우리 사회는 그렇게 생각하지 않는 것 같습니다. 저런. 내신 최고.
그래서 전 대입 시스템이 정말 싫어요. 나에게 맞지 않는 가면을 억지로 씌우는 느낌입니다.
'Karu's ... > Karu's Story' 카테고리의 다른 글
| 퍼준다고 돌려받진 않아요 (0) | 2021.11.21 |
|---|---|
| 불미스러운 일 (0) | 2021.11.11 |
| 징검다리 (0) | 2021.11.05 |
| 나를 위한 프레임 (0) | 2021.10.29 |
| 나만의 길 (0) | 2021.10.25 |





댓글