환영합니다, Rolling Ress의 카루입니다.
NOCHES 글이긴 한데, 제 탐구 일지이므로 반말로 쓸게요.
"미분 가능하면 연속이다" 라는 명제가 있다. 물론, 이 명제는 참이다. 이 명제를 대우시키면, "불연속이면 미분 불가능하다"가 된다. 명제의 대우이므로, 이 역시 참이다. 그런데, 정말 불연속이면 미분이 불가능할까?
그렇다면, '연속'과 '미분'의 정의를 다시 짚어보자.
함수의 연속
고등학교 교육과정상에서는 '좌극한 = 우극한 = 함숫값'이 성립할 때 그 함수를 연속이라고 칭한다. 더 정확하게 하자면,

이 식이 성립하면 함수 f(x)는 x=a에서 연속이다. 자, 그런데. 고등학교 교육과정상에선 극한을 애초에 엉터리로 정의한다. '한없이 다가가는' 따위의 이상한 표현을 쓰기 때문인데, 전혀 수학적이지 못하다. 난 그래서 고등학교 수학이 싫다. 제곱근에 대한 개념 없이 피타고라스의 정리를 설명하는 느낌이다.
그래서, 엡실론-델타 논법을 가져와보겠다. 새로운 연속의 정의를 살펴보자.

이때 델타가 '0보다 큰' 양수이므로 x≠a여야만 한다. 단순하게, f(x)=x², a=3이라고 해놓고 엡실론을 0.1로 잡아보자.

x의 값을 0.01로 잡았더니, 델타의 값이 0.01보다 크기만 하면 된다. 물론 이것으로 간단히 끝나진 않는다. 극한의 개념을 끌고와서, 엡실론과 델타의 관계를 정리해보자.

|x-3|의 절댓값이 델타보다 작다는 것은, 쉽게 말하면 x와 3의 '거리'가 델타보다 작다는 것이다. 다시 말해, x에 델타를 더한 거리는 3보다 작다. 관계식을 다시 정리해보자.

델타에 대한 멋진 식이 나왔다. 극한과 연속의 정의는, 델타가 "존재하기만 하면 된다"라는 것이었다. 그럼 위 식을 자세히 살펴보자. 엡실론은 양수이므로 근호 안이 음수가 될 수 없다. ∃δ. 엡실론을 아무리 작게 줄여도, ∃δ이다. 델타는 반드시 존재한다. 엡실론-델타 논법에 의해 f(x)=x²은 x=3에서 극한값을 갖는다.

x < 3인 x를 아무리 크게 해도, 엡실론은 아주 작게나마 존재할 것이다. 델타는 그런 엡실론보다 더 작게 존재한다. 그렇다면 이 함수는 뭐다? 그렇다, 연속이다.
미분과 도함수
미분한다는 것은 곧 그래프의 기울기를 구한다는 뜻이다. 아까 예시로 들었던 함수 f(x)=x²의 x=3에서의 미분계수를 구해보자.

미분계수는 평균변화율의 극한값이다. x=3에서 h만큼 더 간다면, f(x)는 얼마만큼 가겠는가. 미분계수도 결국 극한값이기에, 좌미분계수와 우미분계수가 같아야 미분계수가 존재할 수 있다.
미분계수를 일반화하면 도함수가 된다.

f'(x)=2x이다. 기초 지식은 끝났다. 이제 질문을 던지러 가보자.
불연속 함수에서 미분을 하면
미분 불가능한 함수를 세 가지 경우로 나누겠다.



연속인 경우
- 1) 첨점이 있을 때 (y=x)
불연속인 경우
- 2) 끊어져 있을 때
- 3 함숫값이 없을 때 (y=x(x-1)/x, x=0에서 정의되지 않음)
1번이야 좌미분계수와 우미분계수가 달라 미분계수가 존재하지 못하고, 2번은 아예 뭐 미분이라 할 것도 없다. 그런데 문제는 3번이다. 지오지브라로 그려봐도 직선으로 나온다. 사실 부드러운 곡선(smooth curve)상의 한 점이 정의되지 않는 경우에는, 극한값을 이용해서 강제로 미분할 수 있지 않을까?
여기서부턴 고3의 머리가 필요하다. 합성함수의 미분법을 통해 미분하면 안 되는 함수를 강제로 미분해보겠다.

두 함수를 준비했다. 첫째는 f1(x) = x², 평범한 이차함수다. 두 번째는 강제로 분모를 만들어 x=3에서 함숫값이 존재하지 않도록 했다. 즉, 실제 녹색 그래프의 x=3에서는 빈 공간으로 정의된다.
극한값을 구하는 경우라면, 분모와 분자를 약분할 수 있다. 그러나 여기서 주어진 함수식을 무턱대고 약분하다가는 두 함수가 같아져버린다. f1(x)와 f2(x)는 엄연히 다른 함수다. 어쨌든, 두 함수의 x=3에서의 극한값과 도함수를 각각 구해보겠다.

...? 뭐지? 둘이 도함수가 같아져버린다. 물론 마지막 계산 과정에서 약분을 ⓑ까지 하지 않고 ⓐ까지만 한다면 여전히 x=3에서 정의되지 않는 도함수를 만들 수 있다. 그런데 그게...맞나? 솔직히 지금 좀 혼란스럽다.
연속함수임을 증명해보자

뭔가 이상한 낌새가 든다. 첫째, 극한값이 9라고 해서 함숫값을 9라고 단정짓고 계산할 수 있는 것은 아니다. 그건 연속함수일 때만 가능하다. 그런데 지금 연속함수라는 가정을 해서 연속함수임을 증명했다. 순환논법이다. 둘째, 정의역 밖에 대해서 생각하는 게 맞는 건지 의문이 든다. 무리함수 (y=√x)는 x<0, 즉 근호 안이 음수가 되는 구간에선 정의되지 않는다.
....어?
뭐가 맞는 걸까
유튜브에서 'Ray 수학' 채널을 운영하시는 Ray님께선 이렇게 말씀하셨다
수학자들도 모순적인 상황들을 수정하고 또 수정해서 만든 게
현재의 수학이에요.여러분들도 어디가 잘못되었는지는 꼭 한 번
생각해보면서 넘어가시길 바랄게요.
Ray 수학, '로지컬님 보지마세요' 中
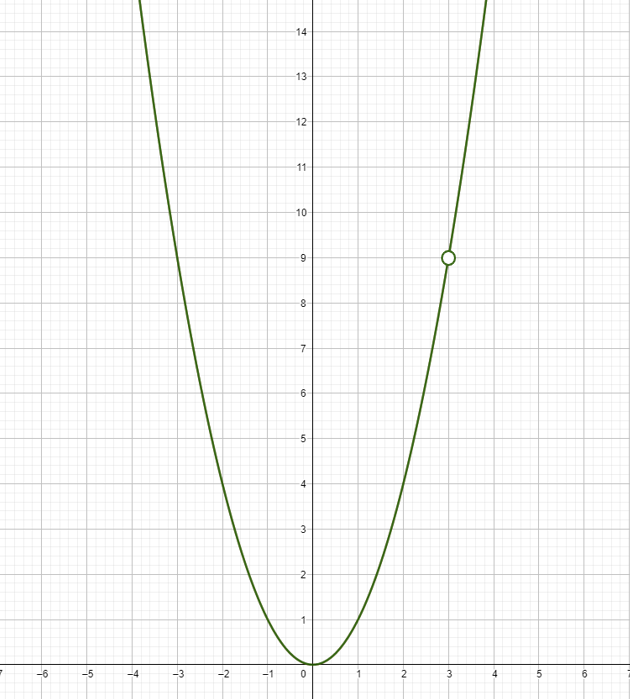

분명 불연속인 함수를 미분했는데, 어째서 실수 전체에서 연속인 도함수가 나온 걸까? 사실, 정의역이 완전히 끊어지거나 하는 게 아닌 이상 smooth curve의 한 점의 함숫값이 없는 걸로는... 충분히 미분 가능해보인다. 위 그래프를 보면, x=3일 때 함숫값이 정의되지는 않았다고 해도 직관적으로 접선을 구할 수 있다. 이런 '추론 미분'은 수학에서 인정해주지 않는 걸까.
일단 정의역을 벗어나서 미분을 하려는 내 시도 자체가 문제 있을 수 있겠다. 그래도, 궁금한 건 꼭 파헤쳐야 직성이 풀리는 타입이라. 당분간 수학선생님들도 내 질문에 같이 고생하실 것 같다.
'학교 > Study' 카테고리의 다른 글
| 스페인어 구문독해 #1 (스페인어권 문화 교과서) (0) | 2022.03.02 |
|---|---|
| 스페인어 속담: Haz bien y no mires a quién & Donde las dan, las toman (0) | 2022.02.18 |
| [수학(상)~미적분] 원의 방정식과 접선, 음함수의 미분법 (0) | 2022.01.12 |
| 국제경제 미수강자의 국제경제 강의 (0) | 2021.12.08 |
| NOCHES를 새롭게 만들어볼까 합니다 (0) | 2021.12.07 |





댓글