환영합니다, Rolling Ress의 카루입니다.
사실 3~8반은 문제 될 게 없어요. 거긴 다 확통이니까. 근데 1반은 미적+사탐방이 꽤 있죠. 사실... 정규분포 곡선 나오는 게 확통에서 나오는 거라 이거 모르면 좀 애를 먹겠더라고요. 그래서, 간단하게나마 설명을 하려고 합니다. 확통을 배우는 게 아니니까, 설명은 미적분을 중심으로 해볼게요.
이 글은 미적분 & 사회탐구방법 수강생들을 위한 글입니다. 확통 하시는 분들은 아마 다 아는 내용일 거예요.

정규분포곡선은 이런 식으로 나타낼 수 있습니다. 여기서 μ는 평균, σ는 표준편차를 뜻합니다. 표준편차는 중학교 때 산포도 배웠으니 아마 알고 계시리라 믿습니다. 자료가 퍼진 정도, 정규분포곡선에서는 그래프가 퍼진 정도를 결정합니다. 평균은 아시죠. 중심의 축을 뜻합니다.

편의상 평균을 m(mean), 표준편차를 s(standard deviation)으로 두었습니다. 지금은 평균이 0, 표준편차가 1인 곡선입니다. 이제 저 m과 s를 적절히 조절해봅시다. 평균을 올리고, 표준편차를 크게 키워볼게요.

참고로 x축과 y축의 비율이 1:1이 아닙니다. 참고하세요. 여튼, 표준편차를 두 배 늘렸더니 그래프가 상당히 퍼졌습니다. 기호로 나타내면 N(2.7, 2²)이 되겠군요. 이제 이걸 가지고 놀아봅시다. 4.4정도의 값을 한 번 그려볼게요.

자, 이렇게 값이 그려졌습니다. 이 값은 전체의 몇 % 구간에 위치할까요? 근데 지금 이렇게 봐서는 좀 복잡합니다. 지난번에 얘기를 했는데, 평균에서 1 표준편차만큼 떨어진 거리 안에 있는 자료들은 전체의 68%라고 했었죠. 강제로 평균을 0, 표준편차를 1로 만드는 겁니다.


이걸 표준정규분포곡선이라고 합니다. 평균과 표준편차를 조절하여 N(0, 1)로 만든 곡선입니다. 최댓값은 x=0에서 0.4네요. 점근선은 y=0. 로지스틱 함수(시그모이드)들 미분하면 이런 모양 나옵니다. 여튼, 곡선은 정규화를 했는데 직선이 가만히 있으면 안 되겠죠. 그래서, 직선도 똑같이 정규화를 해줍니다. 원래 있던 비율상의 위치에 맞춰주기 위해서. 이때 쓰는 게 바로 Z값입니다.

곡선을 표준화시켰다면 그 안에 있던 점들도 모두 표준화를 시켜줘야 합니다. 사탐방으로 치면, 검정통계량과 표본평균 모두를 표준화시켜야 하는 겁니다. 그래서, 저 직선을 안으로 넣어보죠.

이제 한 눈에 보입니다. 첫 글에서 언급했는데, 표준정규분포곡선을 정적분한 값은 1이라고 했죠. 구간 [-1, 1]에서 정적분하면 0.68, 즉 전체 면적의 68%가 나옵니다. 그 말은 곧 저 직선이 전체 자료 중 68%에 해당한다고 볼 수 있겠네요.

표준화 전 곡선과 표준화 전 직선을 비교해도 똑같습니다. 그러니까, 표준화는 결국 모든 정규분포곡선의 모양을 똑같이 맞추어, Z값을 통해 비교를 편히 할 수 있도록 하는 거라고 보시면 되겠습니다.
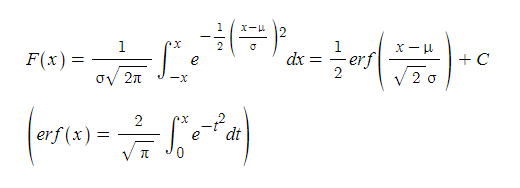
정규분포곡선 적분하면 저런 식이 나옵니다. 근데 딱히 볼 일은 없을 것 같아요. erf(x)는 오차 함수(error function)이라고 부르는 함수가 있습니다. 그냥 넘기세요.
p값이 H0이 참일 때 표본 평균의 분포를 검토하는 거라고 했죠. 유의수준이 임계점이 되고 표본평균이 이걸 넘어가면 이상치가 됩니다. 맞아요. 1.96이니 뭐니 하는 그 Z값이 바로 표준화 된 표본평균입니다. 그게 양 끝단으로 가면 H0을 기각하고, H1을 수용하게 되는 겁니다.
'학교 > Studies' 카테고리의 다른 글
| [미적분] 암기하면 편한 적분 공식들 (0) | 2022.07.17 |
|---|---|
| [사회통계/데이터과학] 4. 회귀분석과 결정계수 R², 추정값 β (0) | 2022.04.20 |
| [사회통계/데이터과학] 2. 표본과 가설검정, p-value와 정규분포 (0) | 2022.04.19 |
| [사회통계/데이터과학] 1. 정규분포곡선의 의미와 해석 (0) | 2022.04.19 |
| 언어학 탐구 프로젝트 #4: 통사론 (0) | 2022.03.19 |





댓글