환영합니다, Rolling Ress의 카루입니다.
전수조사는 정확합니다. 그러나 시간과 비용이 많이 들죠. 단적인 예로, 여론조사 하자고 우리나라 국민 전부를 조사할 수는 없는 일입니다. 그래서, 우리나라 국민들을 **무작위 추출하여 표본을 만들고, 이 표본을 분석하여 우리나라 국민 전체(모집단)에 적용하고자 합니다.
**고등학교 교육과정에서는 무작위 추출만 알고 있어도 됩니다. 표본을 추출하는 방법은 많은데, 알 필요는 없어요.
중심 극한의 정리에 의해, 모집단의 분포와 상관 없이 표본 평균은 정규 분포를 이룹니다. 모집단의 분포에 상관 없이, 표본평균의 분포가 정규분포로 수렴하므로 z값을 통해 확률을 구할 수 있는 거죠. 이걸로 네이만-피어슨 가설 검정을 할 수 있게 됩니다.
상자에 귤 9개와 토마토 1개가 들어있습니다. 이걸 어떻게든 확실하게 판단을 내리고 싶어요. 설사 그 판단이 틀리다고 할지라도. 그래서, 이렇게 씁니다.
상자에서 무언가를 꺼내면 귤이 나온다.
(틀릴 확률 10%)
맞는 말이죠. 10번 꺼내면 10번 중 한 번은 토마토가 나오니, 틀릴 가능성이 10%입니다. 틀릴 가능성, 틀릴 확률. 감이 오시나요? 네, 여기서 말하는 "틀릴 확률"이 바로 유의 확률(p-value)입니다.
귀무가설과 대립가설 얘기는 간단하게만 하고 넘어가겠습니다. 대립가설은 우리가 연구하고자 하는 것, 상관관계를 밝히고자 하는 것을 귀무가설로 잡는 겁니다. 반대로, 귀무가설은 우리가 정한 것과 반대로 세웁니다. 왜 이렇게 할까요? 옳은 걸 증명하기보다, 틀린 걸 증명하는 게 더 쉽기 때문입니다. 내가 세운 가설이 맞다는 걸 증명하는 건 어려워요. 그러니, 내 가설의 역이 틀렸다는 걸 증명함으로써 내 가설을 증명합니다.
귀무가설, H0은 우리 사회 속에 이미 자리잡은 상식이나 일반적인 지식을 말합니다. "A와 B는 관계가 없다" 따위의 형태를 갖습니다. 반대로 대립가설, Ha(H1, H2, ...)은 우리가 연구하고자 하는 것이죠. 귀무가설이 기각되면 얘는 자동으로 채택됩니다. "A와 B는 관계가 있다"의 형태를 가져요.
가설 검정의 원리는, 틀릴 확률을 일단 무시하고 결정을 확실하게 내리는 겁니다. 틀릴 확률이 아주 작다면, 무시해도 되겠지요? 그런데 얼마나 낮아야 할까요. 그게 바로 유의 수준입니다. 유의 확률은 잘못 판단할 가능성입니다.
유의 확률은 p로 표기하며, 틀릴 확률을 뜻합니다. 표집오류, 우연성이란 단어와 함께 기억하면 쉬워요. 내가 관찰하고 있던 게 하필 우연이 일어나서(우연성) 결과가 이상하게 나왔다든지, 전국 학생들 대상으로 설문조사를 하는데 하필 무작위로 고른 게 전부 다 우리 학교 학생이라든지(표집오류), 이런 이상치를 p-value로 표현합니다.
유의 수준은 무시할 수 있는 p-value의 최대치를 뜻합니다. (임계점) α로 표기하겠습니다.
다만, p값 자체를 가설 검증에 쓰면 안 됩니다. 나중에 얘기를 하겠지만, 사실 p값도 T, F, 등등에서 추출된 값이기 때문에 연관성이 있긴 있어요. 그런데 이 개념을 이렇게 외우면 안 됩니다. p-value란, H0이 참일 때 표본평균의 분포를 검토하는 겁니다(내가 관찰한 표본이 매우 특이한 표본일 가능성). 모집단에 대한 확률이 아닙니다. H0이 참일 확률을 판단하는 게 아닙니다.
유의 수준의 값은 몇 가지가 있는데, 주로 0.5, 0.1, 0.01을 사용합니다. 표기는 아래와 같이 합니다.
* p < 0.05
** p < 0.01
*** p < 0.001
자, 그럼 지난 글에서 봤던 표준정규분포곡선을 가져옵시다.
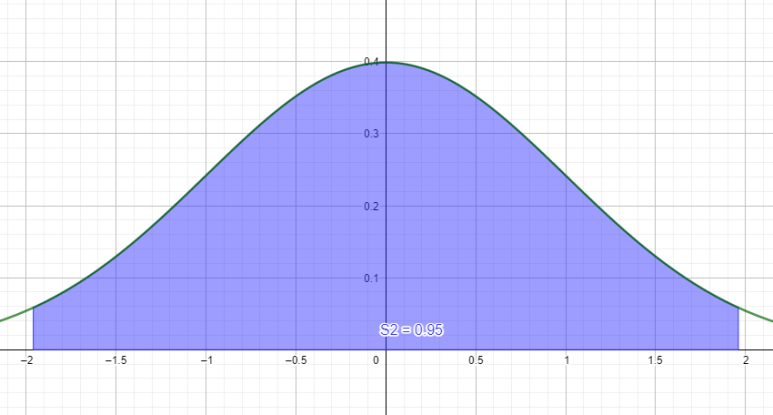
x축은 검정통계량(연구자가 표본을 통계처리 한 값)이 됩니다. 지난번에 살짝 언급했는데, 파란색 영역은 H0 채택역(H0이 기각되지 않는 영역)입니다. 이 범위를 벗어나면 H0이 기각되고, Ha가 채택됩니다.
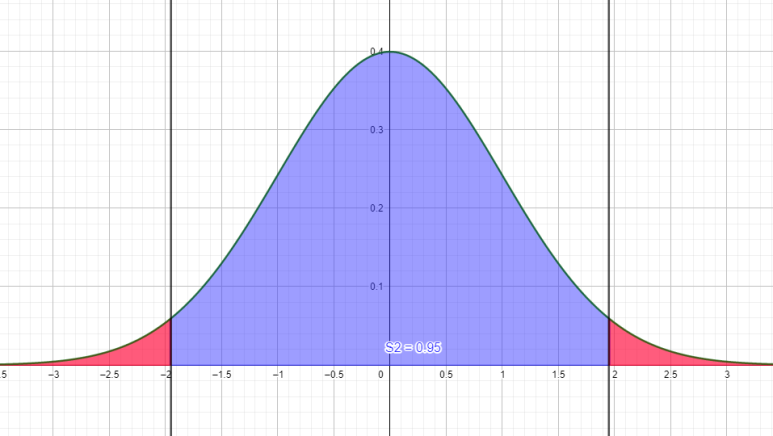
이제 머리를 좀 굴려야 합니다. 이 함수를 정적분해보세요. 유의수준을 0.05로 설정했을 때, 파란 부분이 전체 면적의 95%가 되죠. 그렇다면 저 빨간 부분의 합이 5%, 즉 0.05가 됩니다. (표준정규분포곡선을 정적분하면 1이 나옵니다. 즉, 퍼센트 자체가 면적이 됩니다)
아까 p값은 H0이 참이라는 전제 하에 표본평균의 분포를 관측하는 것이라고 했죠. 그래서 기준은 H0입니다. 그럼 이제 z값, 표본평균의 표준화 값이 어디에 들어가는지 확인해야겠지요.
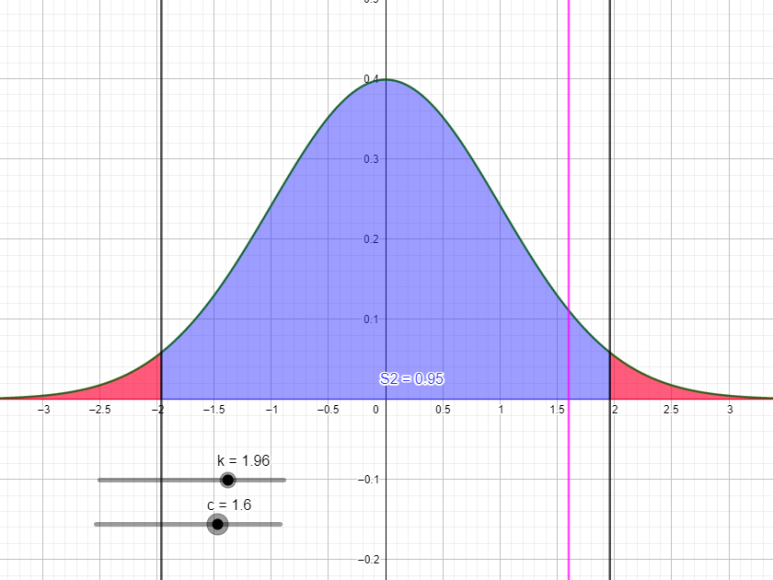
유의수준 0.05에서 만약 표본평균, z값이 [-1.96, 1.96]에 속한다고 생각해보세요. 그러면... 여기는 H0 채택역이죠? 연구자가 제시한 가설은 기각됩니다.
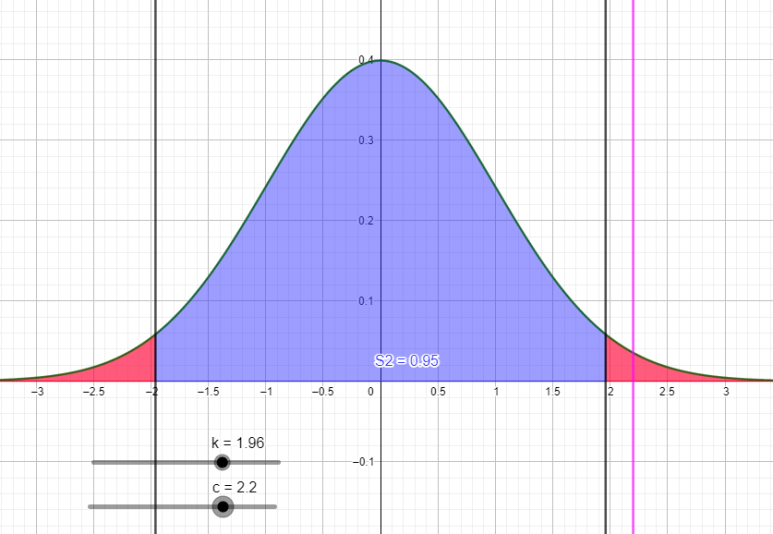
반대로 z값이 2.2정도라고 생각해봅시다. 빨간 구간 안에 들어가네요. H0 입장에서는 이상치입니다. H0이 기각되고, 대립가설 Ha(H1, H2, ...)가 채택됩니다.
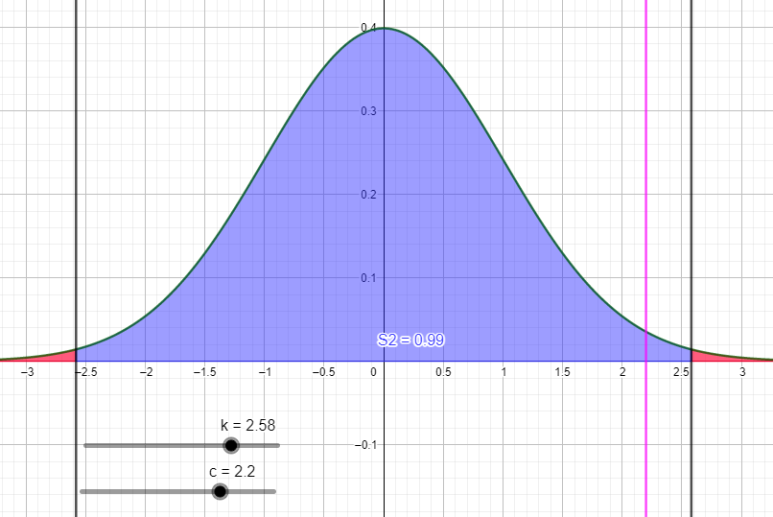
유의 수준을 0.01로 낮췄습니다. 이제 파란색 부분의 넓이는 전체의 99%가 됩니다. z값 임계점(회색 직선)이 양쪽으로 밀려난 걸 볼 수 있죠. H1을 수용하기 까다로워진 겁니다. 대신, 유의 수준이 낮아지는 만큼 잘못 판단할 확률도 줄어들겠죠. 보세요. z값은 아까와 같으나, 유의수준을 낮췄더니 H0 채택역에 들어와버립니다. 이러면 Ha가 기각되는 거죠.
'학교 > Study' 카테고리의 다른 글
| [사탐방/데이터과학] 4. 회귀분석과 결정계수 R², 추정값 β (0) | 2022.04.20 |
|---|---|
| [사탐방/데이터사이언스] 3. 정규분포곡선의 표준화 (feat. 미적분) (0) | 2022.04.20 |
| [사탐방/데이터사이언스] 1. 정규분포곡선의 의미와 해석 (0) | 2022.04.19 |
| 언어학 탐구 프로젝트 #4: 통사론 (0) | 2022.03.19 |
| 언어학 탐구 프로젝트 #3: 형태론 (0) | 2022.03.19 |





댓글