환영합니다, Rolling Ress의 카루입니다.
길게 설명하진 않을게요. 요점만 정리하겠습니다.
회귀분석이란 독립변수와 종립변수의 관계를 밝히는 것입니다. 단순히 "관계가 있다!"로 끝나는 게 아니에요. 그럴 거면 그냥 상관분석(-> [-1, 1]) 쓰면 되죠. 회귀분석은, 무엇이 원인이고 무엇이 결과이며, 정확히 어떤 관계가 있는지 분석합니다.
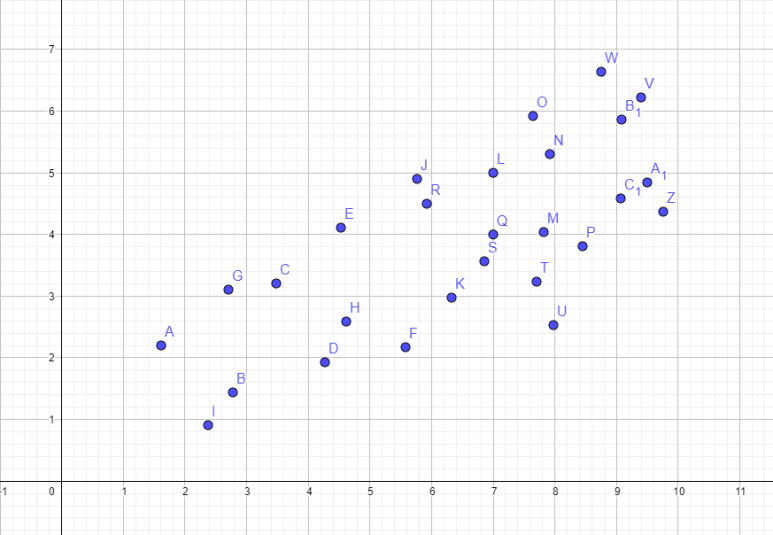
자, 이런 데이터가 있다고 생각해봅시다. 어차피 회귀분석은 독립변수와 종속변수가 모두 양적자료(연속형 변수)일 때 수행하기 때문에 그냥 수학적으로 접근하는 게 편합니다. 이름은 적당히 붙이세요. 가령 x축을 키, y축을 몸무게라고 보든가. 좌표축에 써진 숫자는 무시해도 좋아요.
여튼, 회귀분석은 이들의 관계를 수학적으로 분석하는 겁니다. 쉽게 말해서, 임의의 독립변수 x가 주어졌을 때 종속변수 y를 예측할 수 있게끔 하는 겁니다. 이거 저도 머신러닝에서 꽤 쓰는 건데, 사탐방에서 만나니 반갑네요. 어쨌든, 주로 배우는 단순 (선형) 회귀분석이란 x와 y의 관계식, 즉 함수를 찾아내는 겁니다. 여기서 이 점들의 분포를 가장 잘 따르는 직선을 하나 그어봅시다.
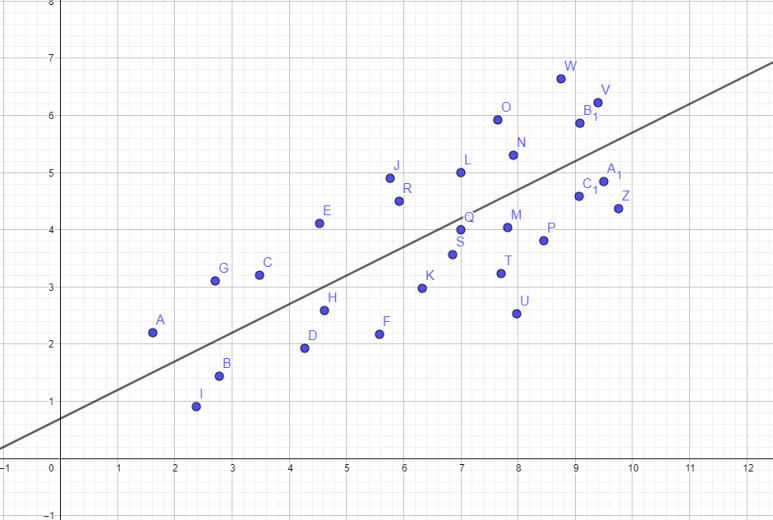
대강 이런 식으로 나오겠죠? 이건 제가 임의로 그린 건데, 실제 회귀분석을 진행하면 더 정교한 값이 나올 겁니다.
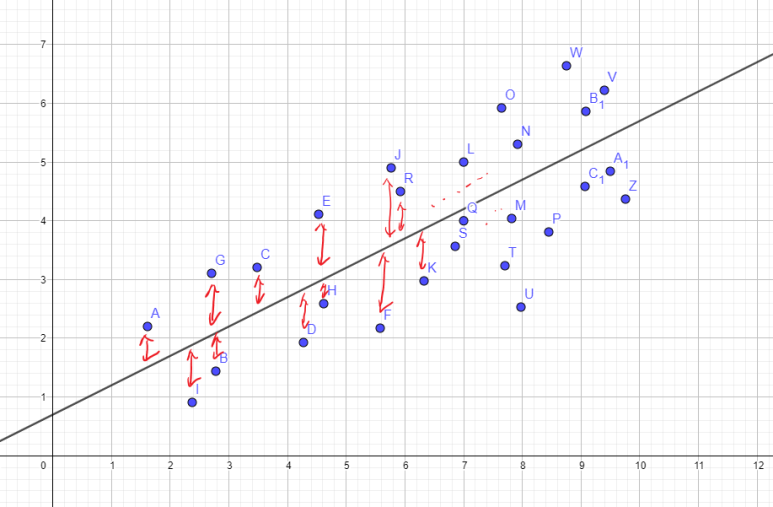
자, 이런 측정 데이터들과 회귀분석의 결과로 나온 직선(회귀직선이라고 하겠습니다)이 완벽히 일치하진 않습니다. 당연하죠. 사회현상은 그렇게 수학적으로 딱딱 들어맞지 않아요. 그러니, 대략적인 추세만 보는 거죠. 여기서 빨간색 화살표로 표시한 부분, 데이터가 회귀직선에서 떨어진 거리를 잔차라고 합니다. 관측(측정)한 값과 회귀 모형으로 추정된 값(직선)이 어느 정도 차이나는지 보여주는 거죠. 잔차는 안 좋은 겁니다. 잔차가 크게 튄다는 건 예외가 있다는 뜻입니다. 이런 표본이 늘어날수록 신뢰하기 어려워지겠죠?
p값은 제쳐두고(어차피 산출되는 값이니), 회귀분석에선 R², 결정계수가 중요합니다. 설명력인데, 회귀 직선이 전체 데이터를 얼마나 잘 설명할 수 있는지 뜻합니다. 쉽게 말해서 결정계수가 1에 가까울수록 데이터가 직선에 몰려있는 거예요.

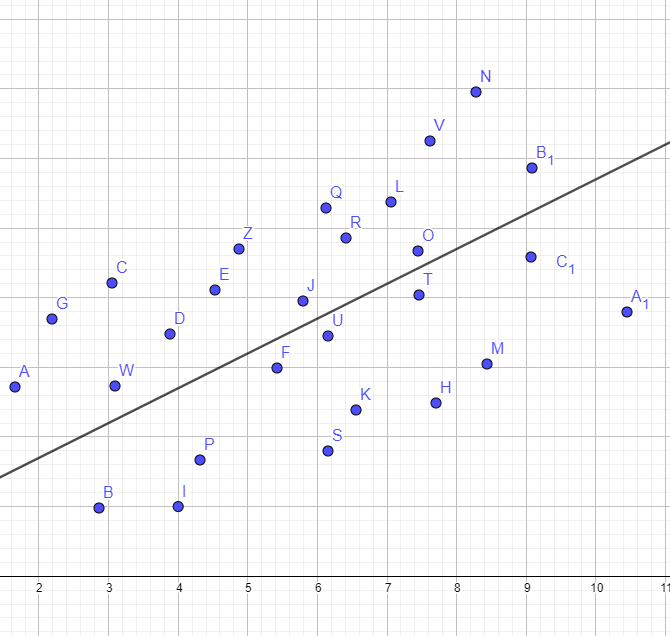
왼쪽과 오른쪽의 그래프를 비교해봅시다. 어느쪽이 직선에 더 몰려있나요? 왼쪽이죠. 왼쪽이 결정계수가 1에 더 가깝습니다. 즉, 독립변수로 종속변수를 추측하기 쉽습니다. 설명력이 높은 겁니다. 오른쪽은 정확히 반대죠. 결정계수가 0에 가깝고, 설명력이 떨어집니다.
보통 R²의 값은 0.1~0.15 정도입니다. 그만큼 사회과학이 딱딱 들어맞지 않는다는 소리이기도 해요. 여튼, 결정계수는 예측의 정확도를 알려줍니다. "몇 %의 설명력을 갖는지."
마지막으로, 비표준화계수 B와 표준화계수 β에 대해 알아보겠습니다. 이거 그냥 추정치입니다. 방금 직선 구했잖아요? 회귀 직선으로 예측한 값(기울기, 상관관계)이 B입니다. B > 0이면 정(+)의 상관관계를, B < 0이면 부(-)의 상관관계를 가지는 거죠. B는 어떤 상관관계가 있는지 알려주는 겁니다. 독립변수를 수준 1만큼 증가시키면 종속변수는 B만큼 증가/감소합니다. 그럼 표준화 계수는 뭐냐? 이것들을 표준화시킨 거예요. 독립변수가 여러 개 있을 때, 표준화계수 β값이 크면 클수록 해당 변인이 다른 변인에 비해 더 큰 영향력을 갖는 겁니다.
아까도 말했지만, 회귀분석의 설명력을 판단하기 위해선 R²을 봐야 합니다. 그럼 F값의 p-value는 언제 보냐고요? 그건 맨 처음에 봤어야죠. 일단 p < 0.05라는 걸 가정하고 분석하는 겁니다. p값이 저걸 벗어나면 굳이 저 결과를 해석할 필요도 없어요. 대립가설이 기각되어버렸는데.
일반적으로 회귀분석은 다음과 같은 과정을 통해 이루어집니다.
1) 회귀식 전체의 유의성을 판단합니다. F값의 유의도 검증을 실시합니다.
2) 독립변수의 B(비표준화계수) 또는 β(표준화계수)의 유의성을 검증합니다.
3) 논문에서의 필요 목적에 따라 비표준화 계수는 회귀식 계수로, 표준화계수는 유의한 독립변수들의 상대적 영향력 크기를 비교합니다.
4) 모형의 적합도를 검증합니다. 결정계수의 크기를 보고 판단합니다. 이때 독립변수간의 관계가 의심되면 문제가 될만한 값들을 빼주고 "수정된 R²" 계수를 보고 판단합니다.
** adj.R²: 수정된 R²: Durbin-Watson 계수를 같이 사용함.
회귀분석에서는 독립 변수들간에 관계가 없다(등분산)를 전제로 하는데, 실제로 그러지 않는 경우가 있다. 그래서 이를 적절히 조절하기 위해 수정된 결정계수를 사용한다. 더빈 왓슨 계수가 2에 가까우면 독립변수간에 관계가 없다는 뜻이 된다. 즉, adj.R²을 사용하는 경우 Durbin-Watson 계수가 2에 가까운 것이 바람직하다.
'학교 > Study' 카테고리의 다른 글
| Project Cylinder 실험 과정 및 절차 안내 (0) | 2022.05.29 |
|---|---|
| [Project Cylinder] 대화형 인공지능 실험 참여자 모집 안내 (0) | 2022.05.29 |
| [사탐방/데이터사이언스] 3. 정규분포곡선의 표준화 (feat. 미적분) (0) | 2022.04.20 |
| [사탐방/데이터사이언스] 2. 표본과 가설검정, p-value와 정규분포 (0) | 2022.04.19 |
| [사탐방/데이터사이언스] 1. 정규분포곡선의 의미와 해석 (0) | 2022.04.19 |





댓글