환영합니다, Rolling Ress의 카루입니다.
우리 학교 교육과정 중에 제가 좀 마음에 들지 않아하는 부분인데, 미적분이랑 확률과통계가 선택이죠. 사실 이게 예전에는 경제수학(미적분 내용)/영미 문학 읽기로 분화가 되어 선택권이 넓었으나, 지금은 미적러가 확통 수업을 들을 수 없습니다..ㅋㅋㅋㅋㅋ 그래서 저는 방학 때 통계 관련 공부를 따로 했어요.
자, 잡소리 그만 하고 시작하죠. 오늘은 사회탐구방법 과목에서 주구장창 쓰이는 곡선인 정규분포곡선에 대해 알아볼 겁니다. 사실 이것 자체는 크게 중요하지 않은데, 몇 가지 중요한 성질들이 있어요.
**생소한 수학 기호가 많을 수 있습니다. 특히 저 함수식은 몰라도 됩니다. 그래프만 보고 넘어가세요. 식은 이해를 돕기 위한 참고용입니다.
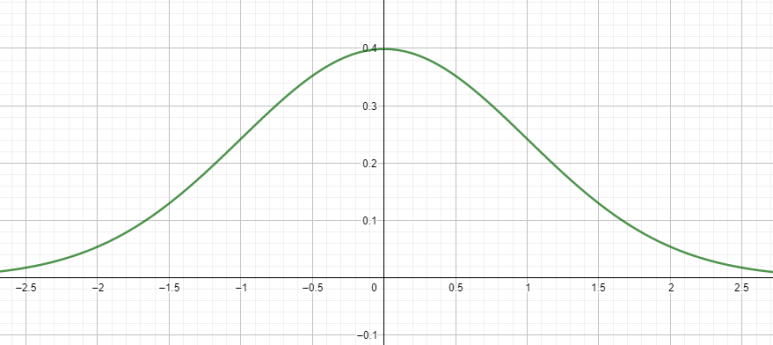
표준정규분포곡선을 그려보겠습니다. 식은 아래와 같아요.

편의상 곡선을 f(x)로 잡았습니다. 참고로, 표준정규분포는 다루기 쉬워요. 이거 전체 적분하면 1 나옵니다. 면적 따질 때 이상한 문자 넣을 필요 없이 전체 면적을 1로 잡고 하겠습니다.
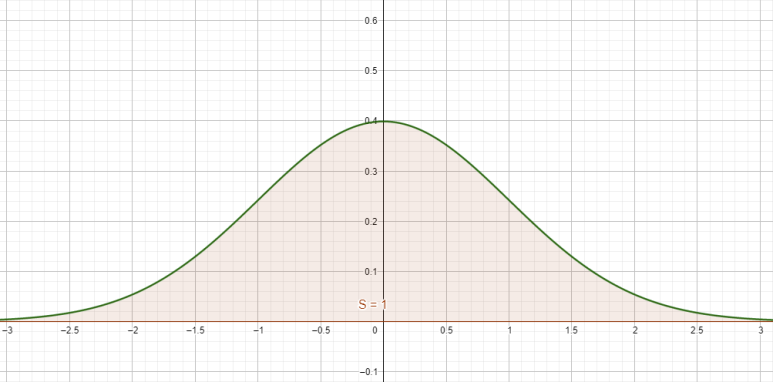
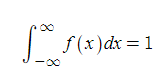
그 다음, 평균과 표준편차가 중요합니다. 각각 μ(뮤)와 σ(시그마)로 나타냅니다. 평균은 이 곡선의 중심을 뜻해요. 위에서는 중심이 x=0 (y축) 이므로 μ=0입니다. 표준편차는 자료가 평균에서 얼마나 많이 떨어져 있는가를 나타내는 것으로, 그래프의 너비를 결정합니다. 참고로 여기선 σ=1입니다.
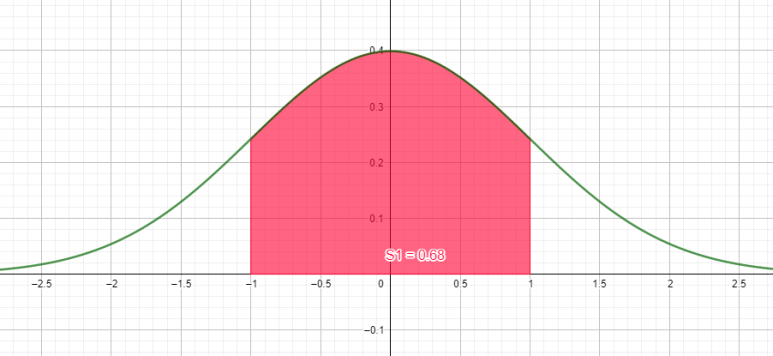
정규분포곡선의 모든 특징입니다. 중심, 즉 평균 μ로부터 좌/우로 각각 σ만큼 떨어져있는 구간의 정적분 값은 전체 정적분 값의 68%입니다. 즉, 전체 자료 중 68%는 평균을 중심으로 표준편차만큼 떨어진 거리 안에 모두 들어온다라고 생각하시면 됩니다.
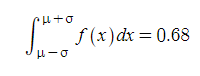
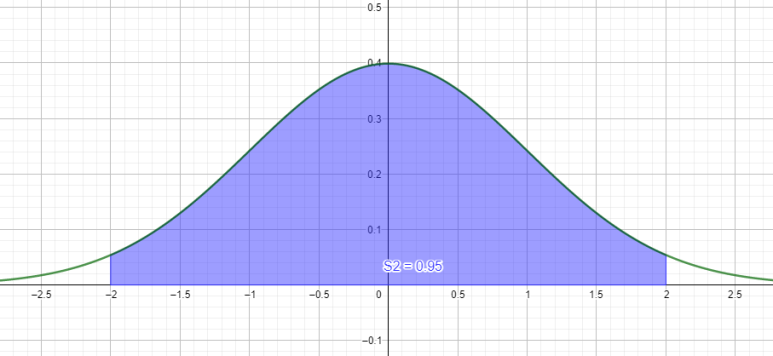
시그마를 두 배로 늘리면 전체 자료의 95.4%가 들어옵니다. 편의상 95%로 하는 경우가 많은데, 95.4%라고 기억해두시는 게 좋아요. 이유는 밑에서 설명하겠습니다. 1.96이라는 수가 어디서 튀어나왔는지 알 수 있거든요.
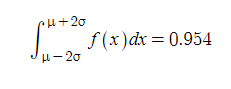
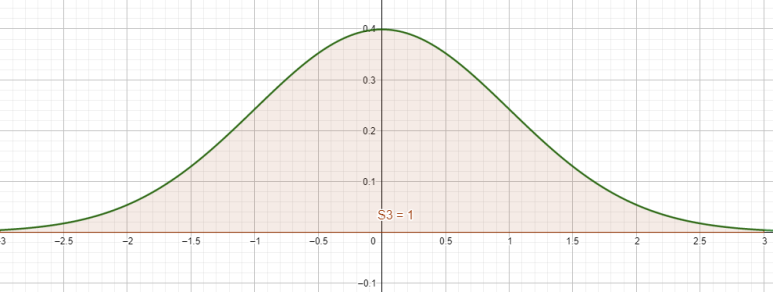
3표준편차만큼 떨어진 거리 내에서는 전체 자료의 99.7%가 들어옵니다. 근데 여기선 반올림했는지 1로만 뜨네요. 99.7%입니다.

자, 그런데 95.4%와 99.7%는 뭔가 애매하단 말이죠. 95%와 99%로 딱 맞추고 싶습니다. 그럼 정적분의 시작점과 끝점을 조절해야 합니다. 다시 말하면, 색칠한 범위의 양 끝을 조절해서 면적을 줄이겠다는 의미죠. 나중에 p값, z값 등 다양한 것들이 나올텐데, 그게 여기서 나오는 겁니다.
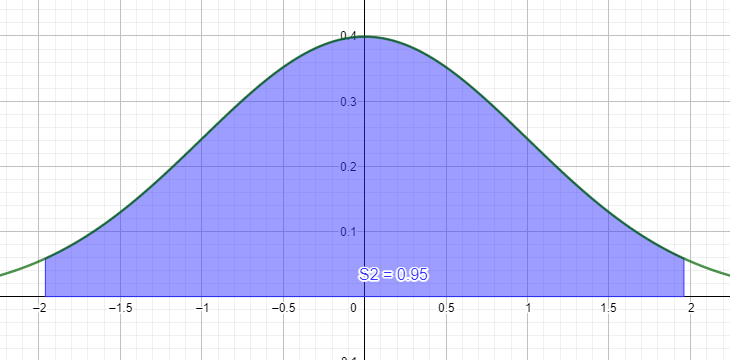
사실 이건 외워두면 편해요. 양 끝을 2가 아니라 1.96으로 줄이면 색칠한 부분의 넓이는 전체 면적의 정확하게 95%가 됩니다. 95%? 맞아요. 나중에 언급하겠지만, 이건 p-value가 0.05일 때 영가설(H0)의 채택역을 나타내는 구간입니다.
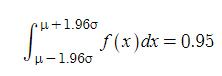
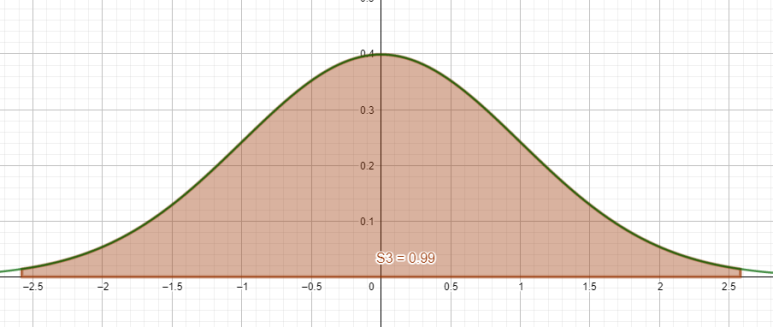
여기도 마찬가지예요. 양 끝을 3이 아니라 2.58로 줄였습니다. 그럼 이 면적은 정확하게 99%가 됩니다. 마찬가지로, 여기도 p-value가 0.01일 때 영가설(H0)의 채택역을 나타내는 구간이 됩니다.
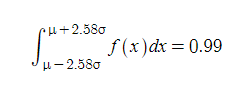
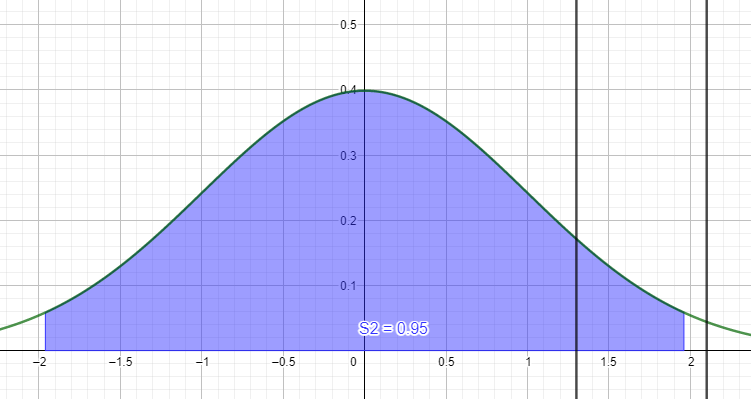
연습문제 하나 보고 갑시다. 유의수준은 0.05입니다. 지금은 표준 정규분포곡선으로 나타낸 거라 x축이 1.96이 되는 지점에서 곡선이 끊겨있죠. 이걸 p값으로 나타내면 0.025가 되는 구간에서 끊길 겁니다. 헷갈릴 수 있습니다. 그냥 비율을 가지고 판단한다고 보시면 됩니다. 만약 유의도 검정을 하는데 p값이 저렇게 S2 안에 들어와버렸다, 그러면 이건 표집 오류가 생긴 겁니다. 반대로 이 범위를 벗어나는 오른쪽 직선의 경우 H0을 기각할 수 있는 거죠.
다만, p값과 Ha의 기각/수용 여부를 따지지 마세요. 사실 연계는 되지만, 그렇게 접근하면 크게 썰리는 수가 있습니다. p값은 그냥 표본 평균의 분포를 나타낸 것에 불과해요. 자세한 설명은 다음 글에서 하겠습니다.
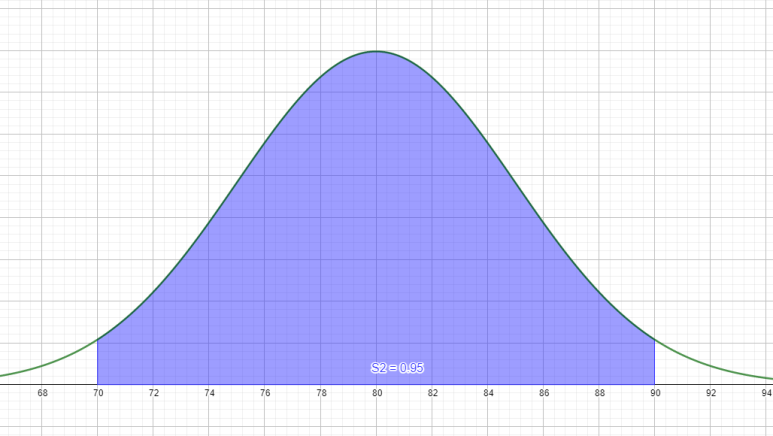
어떤 과목의 평균이 80점, 표준편차가 5라고 합시다. 그럼 2σ, 즉 10점 거리에 있는 학생들이 전체 학생의 약 95.4%입니다. 내가 92점이라면 상위 몇 %일까요? 일단 [70, 90] 범위에 없으므로 95%에 해당하지 않습니다. 그럼 나머지 5%에 속하겠네요. 그런데 왼쪽은 아니죠. 그럼 반띵. 즉, 상위 2.5%에 해당한다는 걸 알 수 있습니다. 정규분포곡선의 표준편차는 이런 식으로 활용하는 겁니다.
'학교 > Study' 카테고리의 다른 글
| [사탐방/데이터사이언스] 3. 정규분포곡선의 표준화 (feat. 미적분) (0) | 2022.04.20 |
|---|---|
| [사탐방/데이터사이언스] 2. 표본과 가설검정, p-value와 정규분포 (0) | 2022.04.19 |
| 언어학 탐구 프로젝트 #4: 통사론 (0) | 2022.03.19 |
| 언어학 탐구 프로젝트 #3: 형태론 (0) | 2022.03.19 |
| 언어학의 이모저모 (1): 언어와 사회 (ft. 속담과 문화) (0) | 2022.03.11 |





댓글