[NOCHES+MATH] 극한의 심화

환영합니다, Rolling Ress의 카루입니다.

​

NOCHES 여러분 안녕하세요! 오랜만입니다. 제가 NOCHES를 대상으로 포스팅을 올린 게 통합과학(아무도 안 봤죠....^^), 스페인어, 경제(1명....^^)였는데, 이번에는 수학을 추가해볼까 합니다. 수학 내신도 낮은 게 웬 수학이냐, 라고 하실 수도 있는데 걱정하지 마세요. 문제풀이나 핵심이 아니라, 개념을 위주로 설명드릴 겁니다. 일단 들어보시면, 제가 왜 이 얘기를 지금 꺼내는지 아실 거예요.

​

저는 고등학교 수학, 특히 수학II를 마음에 들어하지 않습니다. 정확히 말하자면 '수학답지 못하다'라는 생각이 정말 많이 들어요. 예를 들어서 극한의 정의를 살펴봅시다.

$x가\ a에\ 한없이\ 가까워질\ 때,\ f\left(x\right)가\ L에\ 한없이\ 가까워지면\lim _{\combi{x}\to \combi{a}}^{ }\combi{f\left(x\right)=L}$x가 a에 한없이 가까워질 때, f(x)가 L에 한없이 가까워지면limx→af(x)=L​

근데 이 표현 자체가 마음에 안 들어요. "한없이", "가까워진다"라는 게 무슨 뜻일까요? 어...글쎄요. 저도 잘 모르겠어요. 그냥 이렇게 얼렁뚱땅 설명만 하고 넘어갑니다. 그래서 제대로 된 개념조차 잡기 어렵죠.

​

문제를 하나 내겠습니다.

 

"x가 a에 한없이 가까워지면, lim f(x)는 L에 한없이 가까워진다.

맞으면 O, 틀리면 X"

 

정답은 X입니다. "아니, 맞지 않아요?" 글쎄요.

lim f(x) = L, 등호를 썼죠. 같다는 얘기입니다. lim f(x)가 L로 간다는 얘기가 아닙니다. lim f(x)는 L과 정확히 같습니다. 기억하세요. 이걸 모르고 있다간 여러분들은 혼란에 빠지실 겁니다. 극한값은 그냥 저렇게 정의된 거기 때문에, 착각하시면 안 돼요. 0.9999... = 1이 왜 맞냐고 물어보는 것과 같은 맥락입니다.

​

아무튼, 이제 극한을 수학적으로 정의해봐야겠죠. 머리 터지실 수도 있습니다. 적당히 이해만 하고 넘기세요. 원래 대학교에서 배우는 내용입니다.

​ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ...이게 처음 보면 "뭔 소리여?" 하실 수 있어요. 저도 그랬습니다. 식으로만 봐선 이해가 어려워요. 그래프를 하나 들고 오죠.

​

아참, 저 식의 의미는 "적당한 양수 ε(엡실론)에 대해, 적당한 양수 δ(델타)가 존재하고, x와 a의 거리가 δ보다 작지만 0이 아니라면 f(x)와 L이의 거리가 ε보다 작다"라는 뜻입니다.

이런 함수가 있다고 칩시다. 생긴걸 보니 무리함수거나 로그함수거나 뭐 그런 것들이겠죠. 이 함수는 x=a에서 극한값 lim f(x)=L을 갖습니다.

일부를 확대해보면, 이런 모습이 나옵니다. 엡실론을 제시해서 저렇게 파란 구간이 나왔을 때, f(x)가 해당 구간 안에 있도록 하는 x가 나올 수 있도록 적절히 델타를 제시하면 되는 거죠.

​

여기서 논점은, 극한이 존재한다면 엡실론을 얼마로 줄이든 그에 해당하는 델타가 항상 존재한다는 겁니다.

더 확대를 해봐도, 엡실론은 충분히 줄었는데 역시 좌우로 공간이 살짝 남으니까 해당 자리에 델타를 위치시키면 되죠. 어렵지 않습니다.

​

자, 그럼 극한이 존재하지 않는 경우는 어떨까요? 발산하는 경우와 우극한&좌극한 값이 다른 경우인데, 발산하는 경우는 어차피 절댓값 부분에서부터 문제가 생기니 좌우극한을 보겠습니다.

이번 f(x)는 x=a에서 불연속입니다. 극한값도 없겠죠.

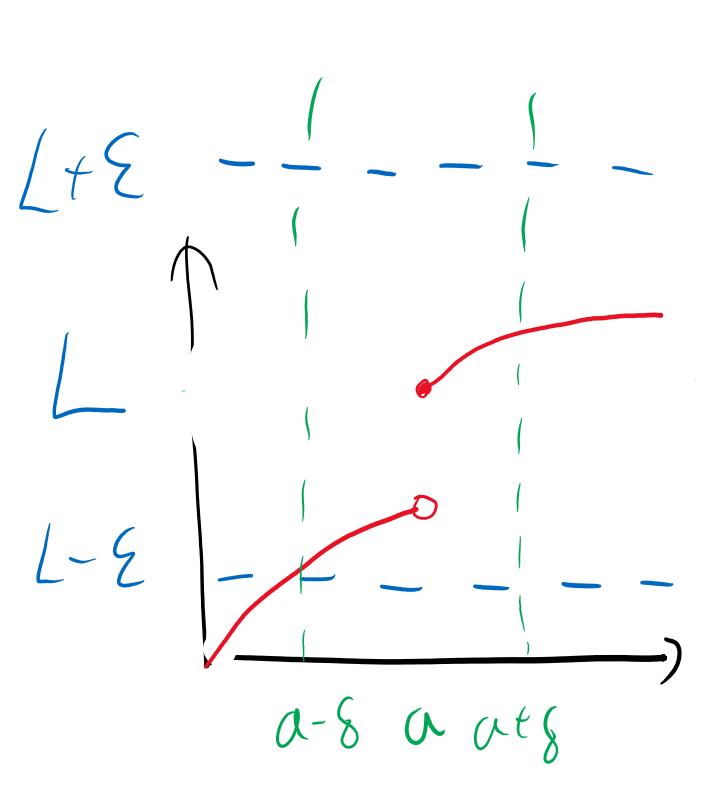
자, 근데 이렇게 하면... 극한값이 존재한다는 결론이 나오게 됩니다. 왜일까요? f(x)가 저 파란 구간 안에 있을 수 있게 해주는 x값이 녹색 구간 안에 있죠?

​

자, 그런데 여기서 중요한 건 얼마나 줄이든지에 관계 없이 항상 델타가 존재해야 극한이 존재한다는 겁니다.

이걸 봅시다. 엡실론을 충분히 줄이니까, f(x)의 그래프가 끊어졌죠. x 값을 찾아봅니다. 일단 어쨌든 실수 전체의 집합에서 정의된 함수이므로 델타 구간에서 x값이 존재하긴 하는데, 그렇다고 해서 해당 구간의 x를 f(x)에 대입했을 때 함숫값이 엡실론 구간에 들어가지 않습니다. 즉, 극한값이 존재하지 않습니다.

​

자, 어떤가요? 오히려 혼란만 드린 게 아닐까 싶네요. 사실...저는 극한이 가장 어려웠습니다. 여전히 배울 게 많기도 하고요. 다음 시간에는 조금 쉬어가는 차원에서 미분에 대해 심화적으로 다룰 겁니다.