환영합니다, Rolling Ress의 카루입니다.
적분이란? 미분이 순간적인 변화를 캐치하는 거라면, 적분은 그 변화를 모두 쌓는 것입니다. 자, 그런데 가끔 일부 학생들이 잘못된 개념을 머릿속에 넣어둔 경우가 많죠.
"아니, 적분은 그냥 미분을 거꾸로 한 거잖아요?"
이것만은 알고 갑시다. 적분과 미분은 별개의 개념입니다. 미분을 거꾸로 한 것을 적분이라고 하자! 이렇게 해서 적분이 나온 게 아니란 말입니다. 실제로 둘의 성질도 아주 달라요. 그리고, 적분이 미분보다 훨씬 먼저 생겼습니다. 그 둘을 이어준 게 미적분의 기본정리인데, 일단은... 넘어갑니다.
적분이라고 하면 보통 정적분을 얘기합니다. 부정적분은 원시 함수를 구하는 것...맞아요. 근데 적분이 도형의 넓이를 구하기 위한 것이므로, 적분은 정적분이 메인이고, 부정적분은 그냥 딸려오는거라고 보는 게 맞아요. 사실 부정적분은 별 거 없죠. 미분 거꾸로 하면 되니까.
오늘은 정적분만 다룰 겁니다. 이 짧은 글에 미적분학의 기본정리까지 끌고오긴 좀 그래서, 일단은 다양한 방법으로 접근할 수 있는 정적분을 봅시다. 정적분을 계산하면 왜 그래프가 이루는 면적이 되는지 보여드리죠.

삼차함수 f(x)가 있습니다. 뭔가 모양이 이상한데, 일단 그렇다고 하죠.

점 a와 b를 잡겠습니다. 이제 f(x), x축, x=a, x=b로 둘러싸인 도형의 넓이를 구해볼 겁니다.
도형의 넓이를 구할 때 가장 중요한 원칙은, 알기 쉬운 도형으로 나누어 계산한다는 겁니다. 우선 이런 방법이 있겠죠.
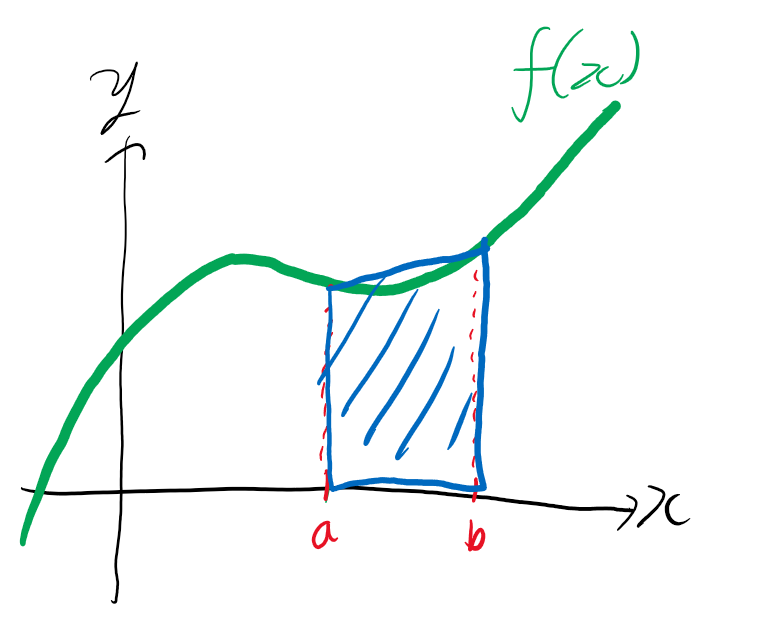
지난 시간에 잠깐 얘기했던 평균변화율을 이용하여 f(x)를 그냥 직선처럼 만드는 법이 있습니다. 그럼 그냥 사다리꼴의 넓이를 구하면 되죠. 쉽고, 간단합니다. 문제는 오차가 생긴다는 거겠죠. 이 오차를 줄여보겠습니다.

4등분을 한 뒤, 막대의 넓이를 각각 더한 후 넓이를 구해주면 됩니다. 이때 높이는 각각의 함숫값, 길이는 |a-b|의 4등분이겠죠. 근데 이 역시도 오차가 있습니다. 이걸 더 잘게 잘라줍니다. 마침내 선으로 이루어지면 어떨까요?

네, a와 b사이를 무한대로 잘게 자르겠습니다. 그럼 셀 수 없이 많은 수의 선분이 나오겠죠. 여기서 각각 선분의 길이는 해당 x좌표의 함숫값입니다. 여기까진 쉽죠.
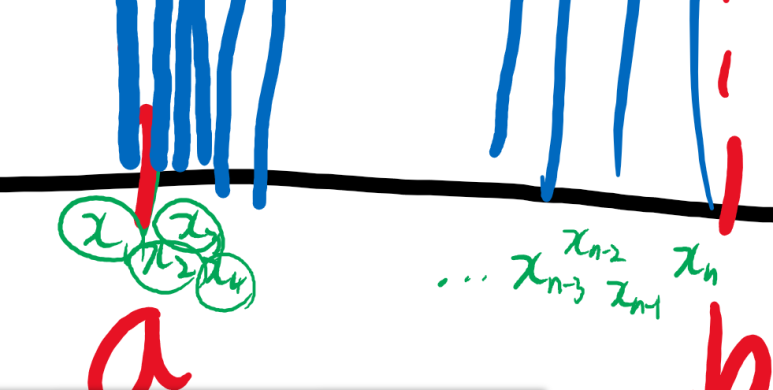
아까 a와 b 사이의 거리를 무한대로 나눈다고 했습니다. 그럼 각각의 x좌표를 x₁, x₂, x₃, ..xn이라고 붙여보죠. 그럼 이제 식을 써 보겠습니다.

우선 n이 무한대로 커져야겠죠.

그리고 이 막대들을 모두 합해야 하니 시그마를 사용합니다. 시그마에 바로 무한을 적용하지 않는 이유는, 잠시 뒤에 n이 또 등장하기 때문입니다.

파란색 부분은 넓이를 구하는 식입니다. 어차피 lim과 ∑가 모든 막대에 대한 계산을 해줄테니, 우리는 막대 하나를 일반화시켜서 값을 구하면 됩니다. 아까 높이는 함숫값이라고 얘기했죠? f(xk)를 넣어줍니다. 그리고 밑변의 길이는 a와 b의 거리를 무한대로 나눈, 즉 (b-a)/n값입니다.
즉, 이 식은 다음과 같습니다.
a와 b의 거리를 무한히 잘게 잘라서, 해당 좌표의 f(x)값 (높이)을 통해
막대의 면적을 구한 후, 그 면적을 모두 합한다.
근데 저 식은 복잡합니다. 그러니까, 줄입시다.

네, lim과 시그마를 줄인 게 저렇게 됩니다. 따지고보면 비슷하죠? 시그마는 합하는 기호입니다. 정적분의 ∫ 기호도 Sum의 S를 늘어뜨린 겁니다. 둘 다 합한다는 면에서 본질적인 속성이 같죠. 그럼 dx는 뭐냐? 저번에 말했듯, 순간적인 변화입니다. 직관적으로 이해가 되지 않는다면 (세로×가로)로 보셔도 됩니다. 아까 직사각형 기억하시죠. f(x)가 그 직사각형의 세로 길이, dx가 가로 길이라고 보셔도 큰 문제는 없습니다. (엄밀하게 파고들면 달라지지만...)
자, 이제 심화 개념은 끝났습니다. 원래 정적분을 정의하려면 유계인 함수에 대해 리만 왼쪽 합과 리만 오른쪽 합이 같다는 걸 증명해야 되는데... 극한이 존재할 조건으로 좌극한과 우극한의 합이 같아야 한다는 건 기억하시죠? 적분도 마찬가지로 상적분과 하적분의 값이 같아야 적분가능하다고 봅니다. 근데 고등학교 과정에서는 그냥 "연속이면 적분가능하다" 정도만 알고 넘어가도 충분합니다. 여러분들께서 중요한 개념들을 헷갈리지 않으셨으면 합니다. 학교에서 배우는 것들 빼고도 좀 더 멀리 볼 수 있다면 좋겠네요.
'학교 > Studies' 카테고리의 다른 글
| [NOCHES+MATH] 다변수함수와 편미분 (0) | 2021.09.29 |
|---|---|
| [NOCHES+MATH] 선형방정식은 계산하지 말자 (0) | 2021.09.28 |
| [NOCHES+MATH] 미분의 심화 (0) | 2021.09.23 |
| [NOCHES+MATH] 극한의 심화 (0) | 2021.09.22 |
| 내가 가장 좋아하는 식들 (수학 / 화학) (0) | 2021.07.20 |





댓글