환영합니다, Rolling Ress의 카루입니다.
수학과의 진로선택 과목으로 <인공지능 수학>이 도입되었습니다. 2015 개정 교육과정의 부분개정으로 추가된 과목인데, 2022 개정 교육과정 (고교학점제)에서도 동일하게 유지되었습니다. 사실 작년에 클러스터로 들을 기회가 있었는데, 예비 번호 받고 떨어졌어요(...) 그래서 어쩔 수 없이 수강하지 못하게 되었습니다. 그래서, 교과서를 바탕으로 핵심 내용만 정리해서 올려보려고 합니다. 단, 기하와 미적분 개념을 같이 사용할 생각입니다. 해당 교과에서도 벡터와 미분에 관한 내용을 다루고 있기에, 이 글을 보시는 분들이 자연계 학생이라고 가정하고 작성하겠습니다.
참고로 수학과 직접적으로 연관만 다루겠습니다. 나머지는 일반적인 검색이나 다른 분야의 도서를 통해 충분히 접할 수 있는 내용입니다. 이에 따라 1단원 내용은 건너뛰겠습니다.
II. 자료의 표현
벡터: 물리학에서는 크기와 방향을 가진 양을 말하지만, 여기에선 선형대수학과 같이 n개의 수를 괄호 속에 순서대로 나열하여 나타낸 것을 뜻합니다. 다만 선형대수학 및 유클리드 기하학과는 다르게 대문자로 표기한다는 게 특징입니다. 평면벡터와 달리, 여기선 성분의 수를 제한하지 않습니다.
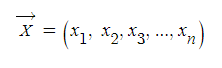
<텍스트 자료의 처리>
단어 빈도수(TF): 텍스트 자료에 단어가 출현하는 빈도수
문서 빈도수(DF): 단어별로 단어가 출현하는 문장의 수
상대도수: DF/n
역문서 빈도수 IDF: n/DF (일반적으로 여기에 log를 취해서 사용)
TF*IDF 의 값을 통해 중요도를 파악할 수 있음.
행렬: 수 또는 문자를 직사각형 모양으로 배열하여 괄호로 묶은 것.
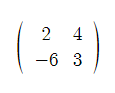
위와 같은 행렬은 2X2 행렬이라고 부른다.
m x n 행렬 A, B에 대해 (단, k는 실수)
A+B: 행렬 A, B의 각 원소를 합해 새로 생성한 행렬 (행렬의 덧셈)
A-B: 행렬 A에서 행렬 B의 원소를 빼 생성한 행렬 (행렬의 뺄셈)
kA: 행렬 A의 모든 원소에 k를 곱해 생성한 행렬 (행렬의 상수배)
m x k 행렬 A와 k x n 행렬 B에 대해
AB: 행렬 A의 i행과 행렬 B의 j열을 차례로 곱하여 더한 값을 (i, j) 성분으로 하는 행렬 (행렬의 곱셈)
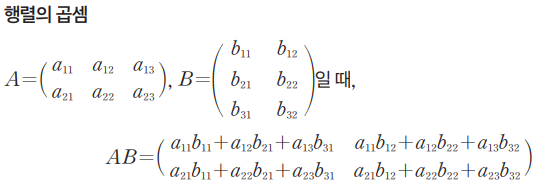
III. 분류와 예측
두 벡터의 유사도를 구하는 법
1) 유클리드 유사도 (벡터의 크기)

기하 내용도 같이 끌고 오겠습니다. 이거 복잡하게 생각할 필요 없이,
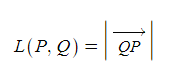
입니다. 보시다시피 원래는 벡터로 나타냈을 때 방향이 바뀌는데, 어차피 제곱을 하니까 신경 안 쓰고 그냥 벡터 PQ로 나타내도 큰 상관은 없습니다. 다만 까다로운 건 이건 평면벡터가 아니라서 성분이 무한히 커질 수 있다는 거. 수식에서 알 수 있다시피, 유클리드 유사도는 두 (위치)벡터의 차를 보기 때문에 0에 가까울수록 두 텍스트가 유사하다고 봅니다.
2) 코사인 유사도

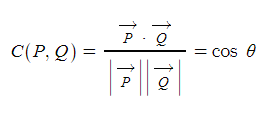
이것도 복잡하게 생각할 필요 없이, 그냥 벡터가 이루는 각을 구한다고 보시면 됩니다. 물론 결괏값은 코사인 값인데, 흔히 알고 있는 두 벡터가 이루는 각의 크기와 같은 공식입니다. (내적의 활용) cos 는 세타가 작아질수록 값이 1에 가까워지죠. 따라서, 코사인 유사도 값이 1에 가까울수록 두 텍스트가 유사하다고 봅니다.
3) 자카드 유사도

|교집합|/|합집합| 입니다. 전체 면적 중 겹치는 면적으로 이해할 수 있으며, 1에 가까울수록 두 텍스트가 유사하다고 판단합니다.
추세선: 산점도에서 두 변량 사이의 상관관계를 파악하기 위해 도입한 직선으로, f(x) = ax+b로 나타낼 수 있다.
IV. 최적화
3단원이 기하(벡터)와 연계되었다면 여기는 수학 II(미분)와 연계됩니다.
손실 함수: 추세선에 따른 오차의 제곱의 평균

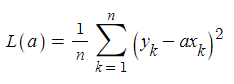
단순하게 분산 구하는 식으로 보면 됩니다. 식을 전개해서 정리하면 기울기 a에 대한 이차함수가 나오게 됩니다. f(x) = ax에 대해 L(a)의 값이 작을수록 f(x) = ax가 그 자료의 예측에 더 적합합니다.
경사하강법(미분을 통해 손실 함수의 최솟값을 찾는 과정)
1) a의 초깃값을 임의로 정한다. (ex: a = 5)
2) L'(a)의 값을 조사하고, 손실 함수의 값이 감소하는 방향을 찾는다.
ex) L'(5) < 0 이면 함수가 감소하므로 다음 a값은 a > 5인 수여야 한다.
3) 새롭게 a 값을 정하고, 이 과정을 반복한다. that is, a=5를 a=10으로 이동시킨다.
이 과정을 반복하다보면 손실함수가 최솟값을 갖게 하는 a의 값을 찾을 수 있습니다.
근데 그냥 미분해서 L'(a) = 0 방정식 풀면 되는 거 아니야?
실전에선 그게 어려울 때도 있으니까.

그런데 얼만큼 이동시켜야 하는지 모르니 적당한 상수 c를 대입합니다.
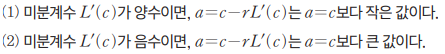
여기서 r은 학습률이라고 합니다. 학습률이 너무 큰 경우 경사하강법을 진행하면서 오히려 함숫값이 올라가버리는(=오차가 커지는) 대참사가 일어날 수 있으며, 학습률이 너무 작은 경우 연산량이 불필요하게 많아지는 단점이 있습니다.
'학교 > Studies' 카테고리의 다른 글
| 수리 면접 대비: 고등학교 화학 개념 요소 정리 (0) | 2022.10.19 |
|---|---|
| 행렬로 연립일차방정식 풀기 (0) | 2022.10.09 |
| 두 직선이 이루는 각의 크기를 구해보자 (ft. cos, tan) (0) | 2022.10.01 |
| 직선의 방정식을 구하는 6가지 방법 (0) | 2022.10.01 |
| 삼각형의 넓이를 구하는 8가지 방법 (2) | 2022.10.01 |





댓글