환영합니다, Rolling Ress의 카루입니다.
다들..학원을 다니시나보네요. 뭔가 그동안 저 혼자 로피탈의 정리를 모르고 있었던 것 같은... 워낙 병기급으로 취급되다보니 어디에서도 이걸 알려주는 곳이 없었습니다. 그래서 그냥 혼자 조사해봤어요.
오늘은 고등학교 미적분을 그냥 종이조각으로 만들어버리는 로피탈의 정리, 이것에 대해 알아보려고 합니다. 내년에 미적분을 선택한 경우, 특히 도움이 될 수도 있습니다. 제 개인적인 견해는, "알고 쓰자"라는 겁니다. 피 보기 전에.
고등학교 물리학Ⅰ을 배우셨다면 아시겠지만, 속도는 변위를 시간으로 나눈 값이죠. 위치를 미분하면 속도가 나옵니다. 이건 수학II에서도 나오는 내용이고요. 속도를 구하기 위해서 변위를 다 측정해야 할까요? 아니요. 그냥 위치의 미분값만 알아도 금방 구할 수 있습니다. "복잡한 계산을 단순화시키자." 이게 로피탈의 정리의 의의입니다.
간단하게 로피탈의 정리를 증명해보겠습니다...만, 해당 증명은 어디까지나 이해를 돕기 위한 설명이지, 엄밀한 증명이 아닙니다. 실제로 로피탈의 정리를 증명하기 위해선 (제가 아주 좋아하는) 엡실론-델타 논법을 사용해야 합니다. 그 내용은 아래에.
엡실론-델타 논법이 뭔지 궁금하시다면 아래 글을 보실 수 있습니다. 근데 머리 터질 수도 있어요.
저는 경고했습니다.
[NOCHES+MATH] 미분의 심화
환영합니다, Rolling Ress의 카루입니다. 지난시간에 극한과 엡실론-델타 논법에 대해 설명해드렸죠. 네...뭐. 고등학교 수학을 풀 땐 그렇게까지 중요한 개념은 아닙니다. 진짜 중요한 건 지금부
rress.tistory.com

자, 이렇게 아주 간단하게 증명이 끝납니다. 왜 이렇게 간단하냐고요? 사실 이 정의는 완전하지 않거든요. 무엇보다, 0/0꼴의 부정형만 가정했어요. ∞/∞꼴은 설명할 수 없습니다. 그런데 제가 여기다가 상세하게 증명을 하면 왠지 여러분들 나가실 것 같아서, 그냥 자제할게요.
로피탈의 정리를 쓸 수 있는 경우

제약이 조금 많아요. 특히 1번에서는 "미분 가능하다"라는 말은 "연속이다"라는 걸 내포하고 있는 거고, "불연속이어도 상관 없다"라는 말은 "미분 가능하지 않아도 상관 없다"라는 뜻입니다. 이 허점을 이용해서, 내신이나 수능에서 로피탈을 쓰면 꼬이게 만드는 경우가 허다하죠. 수학의 본질을 해치는 거니까, 막을 만도 합니다.
로피탈의 정리는 언제 쓰나요? 보통 미정계수를 결정할 때 가장 많이 쓰입니다. 단순히 극한값을 구하는 경우에는, 그냥 극한을 먼저 구해보세요. 그렇게 해서 답이 나오면 쓸 필요 없...아니, 써서는 안 됩니다. 부정형이 아닌 경우에는 로피탈의 정리를 쓰면 답이 틀려요.

여기서 로피탈의 정리를 쓰면 (주어진 식) 부분의 문장이 사라집니다. 인수분해를 할 필요가 없다는 얘기죠.
로피탈을 적용해도 부정형이 나온다면, 부정형이 아닐 때까지 계속 분모와 분자를 미분하면 됩니다.
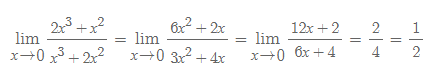
아참, 그렇다고 해서 상수항이 나올 때까지 미분하면 안 됩니다. 위 식에서도 이미 일차식이 나온 순간 부정형이 아니게 됐죠. 부정형이 아닌 식에 로피탈을 쓰면? 틀린 답이 나옵니다.
무한대는 최고차항, 0은 최저차항

이건 너무 자명하죠. 왜냐? 분모/분자를 xⁿ으로 나눠보세요. 그럼 최고차항을 제외한 나머지 항들은 죄다 0으로 수렴해서 사라집니다. 분모, 분자의 최고차항의 계수만 남는다는 거죠. 그래서 답이 저렇게 됩니다.
로피탈의 정리를 사용해도 마찬가지의 값이 나옵니다. 수식은 귀찮아서 안 쓸게요. 계속해서 미분을 하다보면 분모, 분자에 a × n!, b × n! 가 남습니다. 약분하면 역시 a/b죠.

이걸 위아래를 미분해봅시다. 그럼 맨 뒤 일차항은 상수항이 되겠죠. 그리고 나머지 앞의 항들은 죄다 0이 곱해져 소거됩니다. 위 식의 결괏값은 a1/b1입니다. x->0이면 최저차항의 계수비가 됩니다. 이것도 사실 계산할 필요가 없던 거죠.
미적분에서의 로피탈?
쓰다보니까 오비탈이랑 로피탈이랑 헷갈리네요. 오비탈은 화학에서 나오는 거고..

자, 이제 3학년 미적분입니다. 참고로, e^x는 미분방정식 f(x)=f'(x)를 풀다 보면 나오는 식입니다. 눈치채셨죠? 네, e^x=(e^x)'입니다. 미분을 아무리 해도 그대로예요.
즉, 위 식에 로피탈의 정리를 사용하면 분모는 1이 되고, 분자는 그대로죠. 그렇습니다,
양의 무한대로 발산합니다.

얘는 어떨까요? ln x 미분하면 1/x이 나오죠. 네, 0으로 수렴합니다.
아까 속도에 관한 이야기를 했는데, 여기서 알 수 있는 사실이 있습니다.
"x가 한없이 커지면 지수함수가 다항함수보다 빠르고, 다항함수는 로그함수보다 빠르다."
다음을 보세요.

다항함수가 로그함수보다 빠르다고 했습니다. ln t가 무한대로 발산하려는 힘보다 t가 무한대로 발산하려는 힘이 더 세요. 그러니, 극한값은 0에 수렴합니다.
'학교 > Studies' 카테고리의 다른 글
| 국제경제 미수강자의 국제경제 강의 (0) | 2021.12.08 |
|---|---|
| [NOCHES+MATH] 삼차함수 그래프의 개형과 극대/극소 추론 (0) | 2021.10.03 |
| [NOCHES+MATH] 다변수함수와 편미분 (0) | 2021.09.29 |
| [NOCHES+MATH] 선형방정식은 계산하지 말자 (0) | 2021.09.28 |
| [NOCHES+MATH] 적분의 심화 (0) | 2021.09.24 |





댓글