환영합니다, Rolling Ress의 카루입니다.
중간고사가 이제 10일 안팎....우와 긴장되네요. 걍 바로 시작하죠.
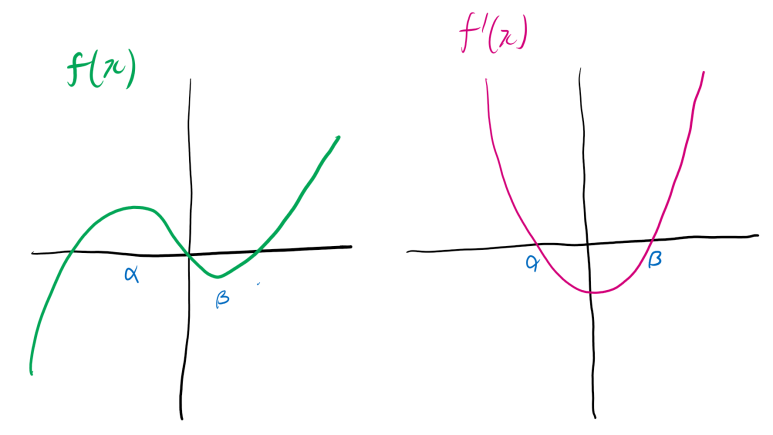
시험범위가 딱 극대극소까지죠. 가끔가다 삼차함수 그래프의 개형을 알아야 할 필요가 생깁니다.

삼차함수는 개형에 따라 실근의 개수가 달라집니다. 그리고 극대극소에서 아주 중요하게 여겨지는 부분 중 하나죠.
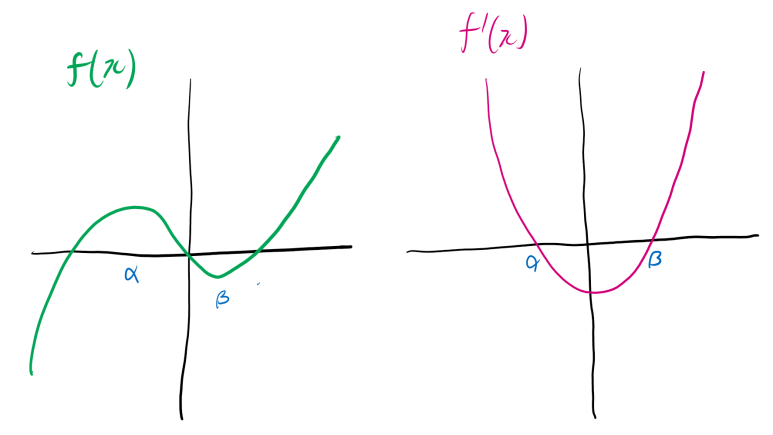
도함수를 통해 함수의 증가와 감소를 판정할 수 있습니다. 여기서 f'(x)=0의 실근을 찾으면 그게 극대, 극소의 x좌표가 되는 거고요. 삼차함수의 그래프의 개형에 따른 도함수를 같이 나타내봅시다.

왼쪽은 삼차함수 f(x)가 갖는 개형입니다. 음의 기울기는 어차피 y축 대칭이니 생략했어요.
함수 f(x)에서 f'(x) > 0이면 f(x)는 해당 구간에서 증가, f'(x) < 0이면 f(x)는 해당 구간에서 감소한다는 건 아실 겁니다. 삼차함수인 경우 도함수가 이차함수이기 때문에 판별이 쉽지만, 사차함수면 살짝 노가다를 해야 합니다.
왜냐고요? 삼차함수 그래프의 개형을 모르잖아요.

만약 최고차항의 계수가 양수인 사차함수 g(x)의 도함수 g'(x)가 위와 같다면, x < a이면 감소, x > a이면 증가, x = a에서 극솟값(=>여기선 최솟값과 같음)을 갖는다는 걸 알 수 있죠.
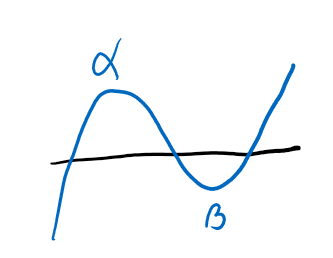
근데 도함수가 이렇게 생겼다면 어떨까요? 어우....난감하죠. 그래서 원래는 미분을 한 번 더 때려야 합니다.

미분해봅시다.
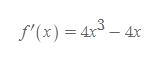
f(x)는 짝수차항으로만 이루어졌으니 우함수, f'(x)는 홀수차항으로만 이루어졌으니 기함수인 것을 알 수 있어요. 대칭성을 생각하면서 접근해봅시다. 별 거 아닌 것 같아 보이지만, 이거 중요해요.

자, 근데 f'(x)가 어떻게 생겼는지 모르죠? 그럴 땐, 미분을 한 번 더 해줍시다.
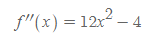
여기서 f''(x)의 판별식을 D라 하고 이 값의 부호를 확인해보죠.

양수입니다. 즉, f''(x)=0은 서로 다른 두 실근을 갖는다는 얘기네요.

빙고, f''(x)의 개형은 이렇게 생겼습니다. 그럼 이제 f'(x)의 개형을 추론할 수 있죠.

그래요, f'(x)는 이렇게 생겼어요. 그럼 f'(x)=0이 되는 x값을 찾아봅시다.

실근이 -1, 0, 1입니다. 그럼 f(x)의 극값들의 x좌표가 -1, 0, 1이란 뜻이겠네요.

f(x)는 대강 이렇게 생겼을 겁니다. x축과의 위치관계는 모르겠지만, 일단 극값들의 x좌표는 저렇겠죠.
그리고, 아까 처음에 f(x)는 y축 대칭 함수라고 말씀드렸습니다. f(-1)=f(1)이에요.
그럼 이제 값을 구해봅시다.

극댓값은 2, 극솟값은 1입니다.
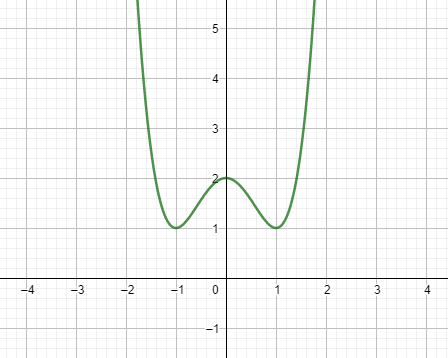
수학 소프트웨어를 통해 f(x)를 나타내보았습니다. 제법 비슷하게 그려진 것 같죠? y축 대칭이라는 것도 정확하게 일치했고, 구불구불한 모양도 정확히 같습니다. 차이점이라면 x축과 만나지 않아 실근이 없다는 것 정도.
'학교 > Studies' 카테고리의 다른 글
| [수학(상)~미적분] 원의 방정식과 접선, 음함수의 미분법 (0) | 2022.01.12 |
|---|---|
| 국제경제 미수강자의 국제경제 강의 (0) | 2021.12.08 |
| [NOCHES+MATH] 로피탈의 정리, 알고 쓰자 (0) | 2021.10.01 |
| [NOCHES+MATH] 다변수함수와 편미분 (0) | 2021.09.29 |
| [NOCHES+MATH] 선형방정식은 계산하지 말자 (0) | 2021.09.28 |





댓글